Review: Mathematical Models Supporting Control of COVID-19

Coronavirus disease 2019 (COVID-19) has had a significant impact on public health and economies worldwide (1-2). Understanding early epidemic trends, providing theoretical support for prevention and control, and evaluating the effect of interventions have been essential foci of COVID-19 research (3-5). Mathematical models play an important role in the study of transmission mechanisms of infectious diseases; dynamic analyses and model-based predictions help guide selection of interventions (6-9). However, classification and applications of existing COVID-19 models are not fully described. For example, some researchers use time-series models to predict epidemic trends, while other researchers use stochastic models for the same purpose (10-12). This situation causes ambiguity in the applicability of models. Classification and applications should be better delineated and standardized, and conditions for appropriate use of specific model types need to be clarified.

For this review we conducted subject heading searches on PubMed and China National Knowledge Infrastructure with search terms “COVID-19,” “Mathematical Statistical Model,” “Model,” “Modeling,” “Agent-based Model,” and “Ordinary Differential Equation Model.” The searches returned 36,021 papers related to mathematical models in the control of COVID-19; 89 are met criteria and are included in this review. We reclassified the models described in each paper, summarized their applications to COVID-19, and analyzed advantages and disadvantages of the models to provide a new classification scheme and a selection basis for future modeling research to further promote use of models in COVID-19 prevention and control.

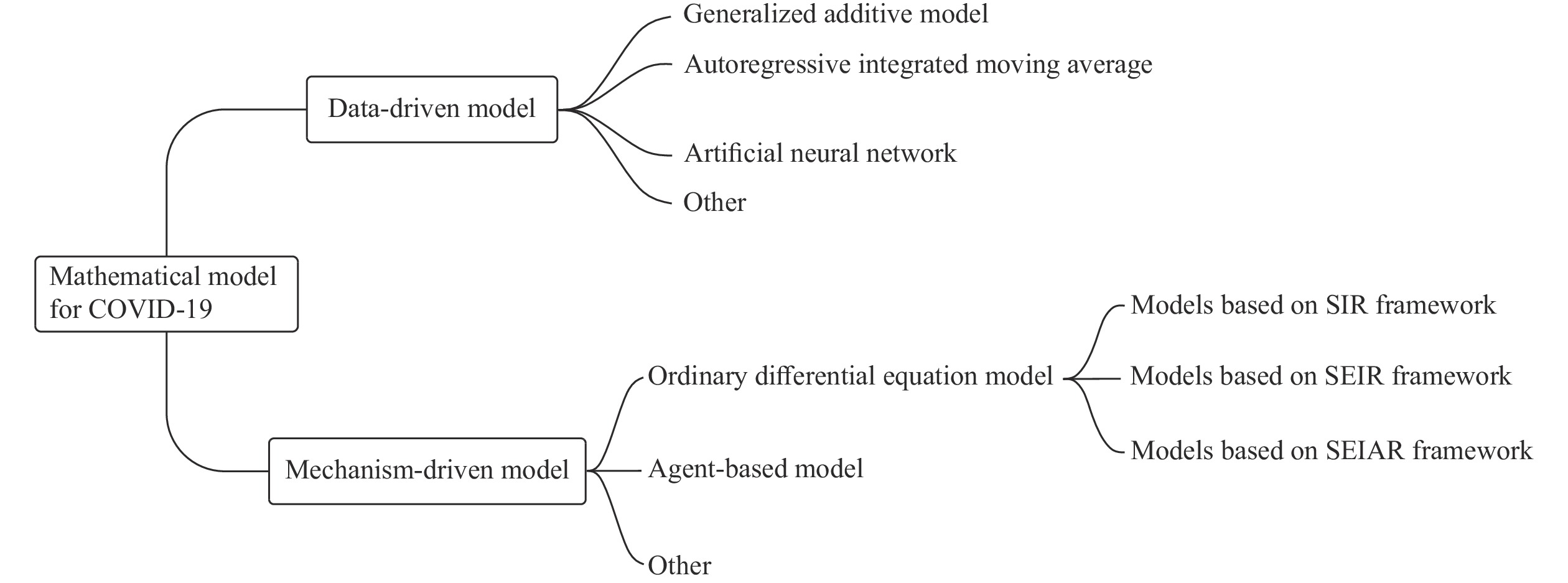
We classified mathematical models as either data-driven or mechanism-driven. Data-driven models include time series models, generalized additive models, and artificial neural network (ANN) models, among others. Mechanism-driven models include ordinary differential equation (ODE) and agent-based models. Figure 1 shows our model classification scheme. In this review, we focus on data-driven, ODE, and agent-based models.

Figure 1. 

Classification of mathematical models in COVID-19.

Abbreviation: COVID-19=coronavirus disease 2019; SIR=susceptible-infectious-removed; SEIR=susceptible-exposed-infectious-removed; SEIAR=susceptible-exposed-infectious-asymptomatic-removed.

“Data-driven model” is a general term for a collection of models that explore the relationship between instances of diseases and time. These models focus on the relationship between number of infections and time and other factors to predict disease trends. Applications in COVID-19 include growth curve models, generalized logistic growth models (GLM), and other real-time prediction models (13-14). These models can be used to describe processes of disease development, evaluate uncertainty of disease incidence, and improve the accuracy of trend predictions (7). Accuracy can be assessed with indicators such as the Akaike information criterion (AIC), Bayesian information criterion (BIC), and r-squared (R²).

Autoregressive integrated moving average (ARIMA) models are autoregressive sliding average models based on time-series data. They have been widely used for COVID-19 predictions (15-18). The basic idea of an ARIMA model is to systematically smooth time-series sampled data to estimate and infer the state of a phenomenon at some future time by revealing the underlying pattern between a target variable and time (19). ARIMA models are adaptable and accurate at predicting trends (20). We found that for COVID-19 research, ARIMA models focused on comparison of predicted time-series data in different regions.

Artificial neural network models have played an important role in COVID-19 prevention and control research (19). ANN models capture uncertainty in time-series data and are a powerful technique for handling nonlinear data, thus complementing traditional linear models and yielding results superior to some other models (21-22). As a stochastic nonlinear recurrent neural network model, the Boltzmann machine (BM) model is a good fit for analyzing cumulative COVID-19 infection data (23-25).

Data-driven models have also been used in other scenarios, including prediction and assessment of cumulative deaths prevented in the pandemic (26-27), optimizing allocation of healthcare resources, and prediction of clinical risk during treatment of COVID-19 (28-30).

ODE models are also known as compartment models (31). They reflect the dynamics of infectious diseases based on occurrence and routes of transmission. ODE models reveal epidemiological routes, predict development trends, analyze key factors of disease epidemics, and seek optimal strategies for prevention and control. The most common ODE model is a system of differential equations based on susceptible-infectious-removed (SIR) and susceptible-exposed-infectious-removed (SEIR) compartments (32). ODE models can be developed by combining population dynamics, vaccination dynamics, isolation, and population exposures (33-34).

The basic reproduction number (R₀) is considered a key variable in ODE models that is related to the spread of infectious diseases (35-36). SIR models have been widely used worldwide, and many studies have calculated R₀ to help predict COVID-19 trends (37-40). SIR models are commonly used to evaluate interventions and calculate transmissibility (41-42). The SEIR model has been used to predict and analyze outbreaks (43-44). It has also been used to analyze transmission mechanisms in different epidemic scenarios and to predict development of an epidemic (45-46). Compared with SIR and SEIR models, the susceptible-exposed-infectious-asymptomatic-removed (SEIAR) model is more applicable for COVID-19 because of its asymptomatic compartment. This model is more suitable for early outbreak predictions (47-48). Developing models for different age groups, genders, and occupations helps scholars understand important differences in the spread of COVID-19 under several scenarios (49).

Developing effective infectious disease prevention strategies requires consideration of disease characteristics, intervention mechanisms, and resource availability. COVID-19 prevention and control measures include non-pharmaceutical interventions (NPIs) and pharmaceutical interventions (PIs) (50-54). NPIs are many, and include isolation, social distancing, wearing masks, and enclosing places of activity (55). In our review, we found that nearly 80% of ODE-based research assessed the effects of isolation, doing so by introducing an isolated population into the base-case model and comparing differences in transmission between isolated and non-isolated populations (11,35–56). Evaluating the effects of other NPIs is achieved by decomposing transmission rate into the probability of transmission of a single contact and the degree of exposure (57). For example, wearing a mask reduces the probability of single-contact transmission, whereas increasing social distance reduces the degree of exposure.

An ODE model that incorporated big data on mobile populations was used to simulate changes in epidemic trends in closed and open cities and provide recommendations for policymakers (58-60). The most prominent application of ODE models of pharmaceutical interventions is to predict a vaccination campaign’s duration, coverage, and impact that will be sufficient to reduce need for NPIs and facilitate recovery of a damaged economy and nation (61). Pandemics tend to decrease only gradually after vaccination (61-62). Key indicators for vaccination campaigns are vaccine effectiveness and coverage attained, with an inverse relationship between the two indicators, so that higher coverage can partially compensate for lower effectiveness (61). Selection of target populations for a vaccination campaign is important. For example, prioritizing vaccination of older age groups is more beneficial for reducing morbidity and mortality (63-64).

Data-driven and ODE models use population characteristics and do not consider heterogeneity of individuals. Agent-based modeling uses a spatial database of the geographical environment of the study area (65) and is usually applied in evaluations of prevention and control measures (10,56–66). These models can refine studies of interventions, demonstrating, for example, that a combination of testing and close follow-up is more effective than mass testing or self-isolation alone (67). Agent-based models makes it possible to evaluate the impact of individual healthcare workers’ hand hygiene practices on COVID-19 transmission (68). To predict trends in individuals’ risk of infection and propose prevention and control strategies, it is necessary to combine individual profiles and demographic data in the model and identify changes in COVID-19 transmission routes in different scenarios (69-74). However, data limitations make it difficult to generalize agent-based model results for prediction of COVID-19 trajectory or evaluation of interventions in a city or country.

Data-driven models have unique advantages in modeling prevention and control of infectious diseases. A wide selection of data-driven models is available, with many featuring ease of use and fast performance for rapid diagnosis in early stages of an outbreak. These models are driven by historical data and statistics and are less affected by parameter changes. However, most data-driven models do not consider natural transmission characteristics and clinical features of the disease. In addition, some key disease parameters lack rigorous interpretation in terms of transmission mechanism or disease etiology, and the models require high-quality historical data, which can challenge assessing effectiveness of some interventions.

Compared to agent-based models, ODE models are more flexible, provide more reliable predictions, and are less computationally demanding. After setting parameters and initial values, ODE models run quickly and are adaptable to the needs of an early and rapid response to a new infectious disease. Additions and deletions can be made according to actual situations, for example, considering different disease states, time-lags, age structures, and birth and death rates. Such adaptations can make the model fit better with reality. The effects of interventions can also be assessed visually by graphing model compartments while changing parameter values. ODE models have some drawbacks. They ignore individual-level heterogeneity and randomness in the disease characteristics; they are not suitable for simulations of epidemics or early cases when some of the parameters are subjective and empirical; and the model results may be realistic and reliable only for the reporting region and may not be generalizable due to regional variability.

By using population characteristics and case data and applying mathematical simulation technology to simulate transmission, agent-based models complement epidemiological evaluation of epidemic characteristics and prevention and control measures (65). A feature of agent-based models is that the results can reflect spatial and temporal characteristics of a disease in the region, as data-driven and ODE models do. A key advantage is that agent-based models are more useful for analyzing infectious diseases transmission mechanisms and estimating infection rates. Shortcomings include that agent-based individual random models require a large amount of well-measured data and require researchers to have geographic environment modeling experience and a strong foundation in programming.

For the COVID-19 pandemic, each type of model has strengths, weaknesses, and a spectrum of applicability to different scientific questions, and each requires varying degrees of background knowledge from the researchers. Infectious disease data-driven models provided information for action by policymakers, clinicians, and public health practitioners during times of great uncertainty about the COVID-19 pandemic. Although most COVID-19 modeling studies used ODE models, as ODE technology advances, future research will involve more cross-pollination between different disciplines. Agent-based models were not widely utilized in COVID-19 prevention and control efforts. Research with more complex and systematic methods has only just begun, and there is still a great deal of in-depth research work to be done in this area.

When dealing with an outbreak of an emerging infectious disease, model selection is based on several points. 1) Stage of the transmission. During the COVID-19 pandemic, different types of models were used at different stages. In the early stages of an epidemic, there is less knowledge about the disease, and therefore only basic SIR or SEIAR models can be built. As the disease is studied and research reveals important insights, it is possible to build more complex models that can perform new and different functions. 2) Data availability. Data are fundamental for building models, and data completeness constrains model selection. When there are insufficient real-world data, researchers can only use basic data-driven models to predict the trajectory of an epidemic. As the amount of data increases and data sources diversify, the type, veracity, and complexity of built models can increase. 3) Applications of the model. When choosing a model, it’s purpose must be clear. For example, to evaluate the impact of prevention and control measures, one must consider the natural history of the disease, characteristics and settings of the intervention, and other factors. To study the influence of individual factors, an agent-based model should be considered. 4) Generalizability of the model. Most modelling studies are set in small areas, and a model appropriate for one setting may not be applicable elsewhere. Therefore, when selecting model parameters, it is important to consider variability of study sites and parameter values in a comprehensive manner.

Our review has shown that many studies have been conducted with COVID-19 mathematical models, and that mathematical models are highly suitable for analyses of the pandemic. Although many types and applications of COVID-19 models exist, we found that the models can be divided into mechanism-driven models and data-driven models, and that model applications are mainly focused on predicting trends, evaluating the effects of interventions, and estimating severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) transmissibility. Models are playing a critically important role in COVID-19 prevention and control. In the future, mathematical models will be used to provide scientific support for evidence-based, innovative, and precise responses to many infectious disease outbreaks.

No conflicts of interest.