Download:
-
On January 20, 2020, the Chinese State Council added the latest coronavirus disease (COVID-19) to the Category B list of nationally notifiable diseases under Category A management (1-2). This means that if a case is diagnosed with COVID-19, it must be reported by the physician to the National Notifiable Disease Reporting System (NNDRS) within two hours. However, new cases reported every day from the surveillance system often contain cases that had onset on or before the reporting date, indicating a lag between onset and diagnosis. A more accurate assessment of incidence will allow public health professionals to better assess ongoing outbreaks, the pattern and scale of further epidemics, and the effectiveness of current prevention and control strategies, etc. (3). However, in the case of an emerging infectious diseases, such as COVID-19, the precise distribution of lag time between the dates of onset and the reporting times at the early stage of transmission was not known due to lack of historical data. Furthermore, all statistical incidence counts of each day are censored or truncated, i.e. up to the last reporting date, making it more difficult to estimate the precise distribution of delayed onset-reporting times. In this study, a Bayesian statistical method was proposed to estimate the exact probability distribution of the lag time between the onset date and the reporting time, and then to predict the actual number of new incident cases and the number of unreported cases per day.
All data for this study were obtained from NNDRS. The dataset for all suspected and confirmed cases of COVID-19 was downloaded from NNDRS around 24∶00 on March 26, 2020, and the difference between date of onset and report time was used to calculate the lag time for each case. The lag time was assumed to follow the same probability distribution over a certain timeframe if the case diagnostic criteria, diagnostic methods, and other factors related to case reporting remained relatively stable. For this reason, new cases with onset dates between February 5 and February 28 were chosen for this analysis, and a training dataset (data reported as February 28 at 24∶00) and a validation dataset (data reported as March 25 at 24∶00) were built. Based on the distributions of time delays for other infectious diseases, particularly influenza cases in the last few years and the empirical distribution of time delays for all COVID-19 cases in NNDRS, the gamma probability distribution was selected to be validated with high priority in this study. At first, the lag times were transformed using the base-2 logarithm. A random variable X that is gamma-distributed with parameters α and β is denoted as follows:
$$X \sim \Gamma \left( {\alpha ,\beta } \right) \equiv Gamma\left( {\alpha ,\beta } \right). $$ (1) Where α is a shape parameter and β is a scale parameter, also called a rate parameter. Its corresponding probability density function is as follows:
$$f\left( {x;\alpha ,\beta } \right) = \frac{{{\beta ^\alpha }{x^{\alpha - 1}}{e^{ - \beta x}}}}{{\Gamma \left( \alpha \right)}}\;\;\;{\rm{for}}\;x > 0\;\;\;\alpha ,\beta > 0 $$ (2) In our study, the logarithms of lag times were assumed to follow the truncated gamma distribution.
$$\begin{aligned} & {log _2}\left( {lagtime\left[ i \right]} \right) \sim \Gamma \left( {\alpha ,\beta } \right)T\left( {0,index\left[ i \right]} \right) \equiv \\ & \quad Gamma\left( {\alpha ,\beta } \right)T\left( {0,index\left[ i \right]} \right) \end{aligned}$$ (3) $$\alpha \sim uniform\left( {9.0,15} \right) $$ (4) $$\beta \sim uniform\left( {3.5,6.5} \right) $$ (5) Where the α and β are the parameters to be estimated for the gamma distribution, the prior distributions of both parameters were set to follow the uniform distributions, lagtime[i] is the logarithm of the lag time of the i-th case, T stands for the truncated distribution, and index[i] is the logarithm of the time interval from the start date of the i-th case to the end of the study time frame (24∶00 on February 28) of the training dataset.
The cumulative reported rate was calculated using the posterior parameters of gamma distribution estimated from the above-mentioned steps and the gamma cumulative distribution as follows.
$$rate\left[ n \right] = F\left( {n;\alpha ,\beta } \right) = \int_0^n {f\left( {u;\alpha ,\beta } \right)} du $$ (6) Where F and f are the gamma cumulative probability function and gamma probability density function, respectively. The number of unreported incident cases was assumed to follow the negative binomial distribution. The number of cases of incidence for each day were estimated as follows.
$$NR\left( n \right) \sim dnegbin\left( {rate\left[ n \right],reported\left[ n \right]} \right) $$ (7) $$NN\left( n \right) = NR\left[ n \right] + reported\left[ n \right] $$ (8) Where n is the number of days from date of onset to the 24∶00 on February 28, the dnegbin is the negative binomial distribution, the rate[n] is the cumulative probability of reporting of n days, the reported[n] is the numbers of reported cases of n days calculated from the training data samples, and the NR[n] is the number of unreported cases, and the NN[n] is the predicted total number of cases. Since the number of new cases reported within two days was almost zero, we estimated the real incident cases from February 5 to February 26, 2020.
The validation data included all the cases with onset dates between February 5 and February 28, which were reported until 24∶00 on March 26. The logarithm of the lag times in the validation dataset were fitted with gamma and other probability distribution models. The parameters of gamma probability distribution were estimated in both the training dataset using Bayesian Markov chain Monte Carlo (MCMC) method with truncated distribution and in the validation dataset using maximum likelihood method, respectively. The parameters of gamma probability distribution from training were used to estimate unreported and total number of incident cases every day. The estimated number of unreported and total incident cases were compared with the actual reported ones in the validation dataset. All statistical analyses were performed in R statistical software (version 4.0.3; The R Foundation for Statistical Computing, Vienna, Austria) (4), where Bayesian statistics were performed using the rjages (5) and runjags (6) packages, and general probability distribution fitting was performed using the fitdistrplus (7) package.
As of 24∶00 on March 26, there were 24,551 cases in the validation dataset with onset dates between February 5 and February 28. The median lag time was 4.92 days, with 25 and 75 percentile values of 3.41 and 8.43 days, respectively. Gamma distribution was found to be the best fitted model compared to other probabilistic distribution models based on either the Akaike information criterion (AIC) or the Bayesian information criterion (BIC) values. The shape and rate parameters of the gamma distribution of the validation dataset were 8.56 and 3.54, respectively (Table 1).
Distribution LogLikelihood Akaike information criterion（AIC） Bayesian information criterion (BIC) Gamma –29,206.3 58,416.6 58,432.8 Burr –29,705.1 59,416.3 59,440.6 Weibull –29,757.8 59,519.6 59,535.8 Normal –30,102.4 60,208.7 60,224.9 Pareto –46,263.8 92,531.6 92,547.8 Table 1. The results of probability distribution fittings of the logarithm of the lagtimes based on validation dataset.
The gamma probability distribution curves obtained for the two different methods as mentioned above are shown in Figure 1.
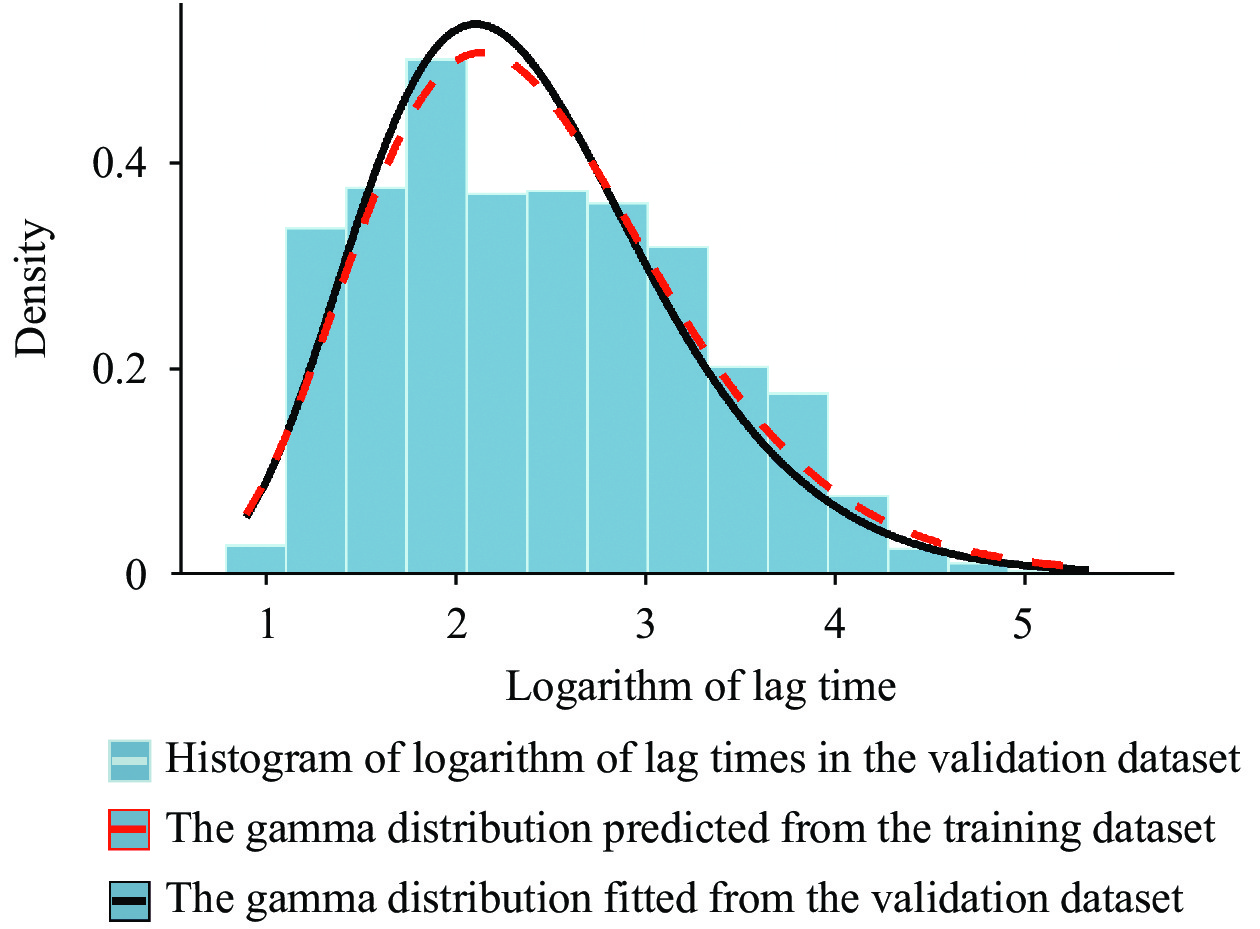Figure 1.Comparison of the curves of the two gamma probability distributions of lag time based on the training and validation datasets.
For the number of cases with an onset date between February 5 and February 26, the model predicted that there would be 2,112 unreported cases, while the actual reporting resulted in 1,665 newly reported cases as of March 26. The number of unreported cases predicted by the Bayesian model was 26.84% higher than the actual number of reported cases, with a ratio of 1∶0.7881.
The model’s prediction of the total number of incident cases per day and its trend from February 5 to February 26 were generally consistent with the actual incidence data reported as of March 26. However, the model’s predictions after February 21 were significantly higher than the actual data reported as shown in Figure 2 and Table 2.
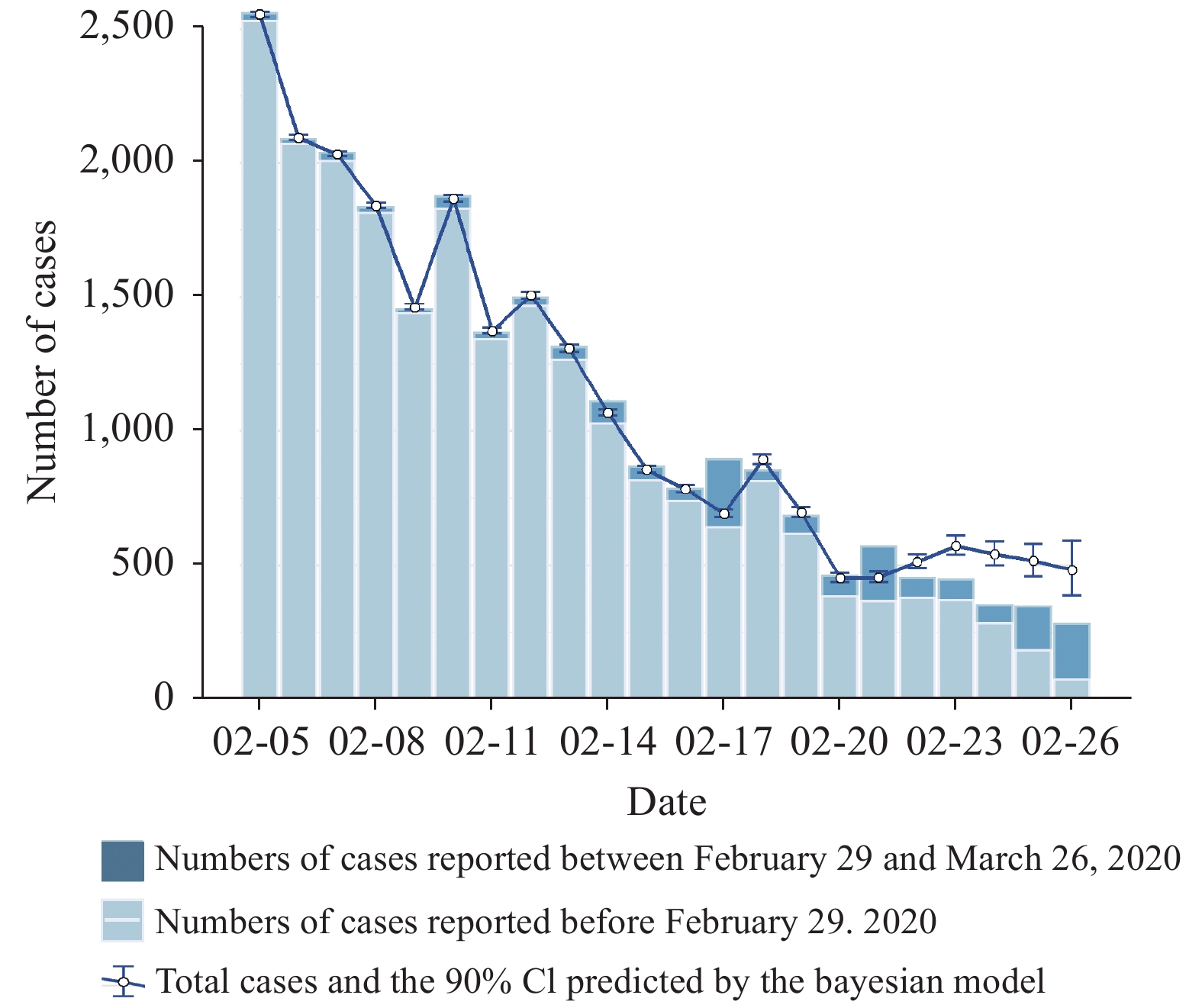Figure 2.Comparison of the predicted number of COVID-19 incident cases by the Bayesian probability model and the number actually reported.
Date of onset Number of incident cases reported by February 28 Number of unreported cases and 95% CI predicted by model Total number of incident cases and the 95% CI predicted by model Number of incident cases reported by
March 26Cases reported
from February 29
to March 262020/2/5 2,529 24(15–34) 2,553(2,544–2,563) 2,559 30 2020/2/6 2,072 22(13–32) 2,094(2,085–2,104) 2,087 15 2020/2/7 2,007 25(16–36) 2,032(2,023–2,043) 2,036 29 2020/2/8 1,814 26(17–37) 1,840(1,831–1,851) 1,833 19 2020/2/9 1,438 24(15–35) 1,462(1,453–1,473) 1,453 15 2020/2/10 1,830 36(25–49) 1,866(1,855–1,879) 1,875 45 2020/2/11 1,343 31(21–43) 1,374(1,364–1,386) 1,366 23 2020/2/12 1,465 41(28–54) 1,506(1,493–1,519) 1,495 30 2020/2/13 1,265 42(30–56) 1,307(1,295–1,321) 1,313 48 2020/2/14 1,027 42(30–55) 1,069(1,057–1,082) 1,111 84 2020/2/15 816 41(29–54) 857(845–870) 868 52 2020/2/16 739 46(33–61) 785(772–800) 787 48 2020/2/17 642 50(37–65) 692(679–707) 893 251 2020/2/18 813 81(64–101) 894(877–914) 851 38 2020/2/19 616 81(63–100) 697(679–716) 684 68 2020/2/20 384 68(51–86) 452(435–470) 461 77 2020/2/21 365 89(70–111) 454(435–476) 570 205 2020/2/22 379 134(109–161) 513(488–540) 452 73 2020/2/23 371 201(167–238) 572(538–609) 445 74 2020/2/24 282 259(217–305) 541(499–587) 350 68 2020/2/25 181 335(277–398) 516(458–579) 347 166 2020/2/26 74 408(314–517) 482(388–591) 281 207 Total 22,452 2,106(1,641–2,628) 24,558(24,093–25,080) 24,117 1,665 Table 2. Comparison of the predicted number of COVID-19 incident cases by the Bayesian probability model and the number actually reported.
HTML
-
We attempted to estimate the actual number of incident cases during an outbreak of a new infectious disease. We assumed that the probability distribution of the lag time between the start date and the reporting time was relatively stable. Based on data from reported cases, the gamma probability distribution, and the Bayesian statistical method for truncated data, the parameters for the gamma probability distribution of lag times were inferred. Using the cumulative reporting rates calculated from the gamma probability distribution of lag time, the number of reported cases, the negative binomial distribution, the numbers of both unreported and total incident cases, and their 95% CI, were predicted. The results showed that the Bayesian probability model predictions based on data reported by February 28, 2020 were similar to those actually reported 1 month later.
The parameters of distributions for the lag reporting time were obtained using two different methods and datasets. The first was inferred from the truncated training dataset using the Bayesian MCMC-based parameter estimation method, and the second was estimated from the actual data reported 1 month later using the maximum likelihood estimation (MLE) method. It was found that both the parameters and the curve patterns of the two distribution models were consistent with the Kullback–Leibler divergence 0.048.
As for the number of unreported cases, the Bayesian model prediction was 26.84% higher than the actual reported number, but the absolute difference was only 1.82% of the total number of cases reported, i.e. (2,112–1,665) / 24,551 × 100%. The total number of incident cases reported by March 26 were within the 95% CI of total number of incident cases predicted by the model.
The number of actual daily reported cases was highly congruous with the predicted number of cases and associated trends between February 5 and 20. However, the model predicted an increase from February 20 to 23, and subsequent reports verified an anomalous increase in the number of cases on February 21 that could have changed the direction and magnitude of the model’s predictions and partly explain why the model’s predictions were higher than the actual reported number. In addition, the model forecast trend for the period of February 23–26 was consistent with the actual report, although the predictions were higher than the subsequent report.
Limitations in the application of this model may arise primarily from the assumption that the lag time distribution from onset to report is relatively stable. This is difficult to achieve in the process of preventing and controlling new infectious diseases. In the case of COVID-19, for example, changes in diagnostic or reporting criteria, improvements in diagnostic techniques, and increased prevention and control efforts may change the interval between onset and reporting, e.g. the use of square-cabin hospitals and the widespread availability of nucleic acid testing have significantly reduced the lag time interval. Second, a small number of cases may have an impact on the stability of the model parameter estimates. Therefore, it is recommended to use national or province-wide pooled data for model parameter estimates at the early stages of an epidemic for new infectious diseases.
In conclusion, this study provides an early prediction method for the actual number of incident cases based on data from the surveillance report, which is of great importance to epidemic prevention and control personnel in estimating the actual occurrence of the epidemic, predicting trends, and assessing the effectiveness of prevention and control measures.
Fundings: This study was supported by grants from the Key Joint Project for Data Center of the National Natural Science Foundation of China and Guangdong Provincial Government (U1611264), The National Major Scientific and Technological Special Project for HIV/AIDS and Hepatitis B prevention (2013ZX10004218-006, 2017ZX10303401-005, 2018ZX10201002), and the National Key Research and Development Program of China (2016YFC1200703).
| Citation: |
|